$ \newcommand{\CF}{\mathcal{F}} \newcommand{\CI}{\mathcal{I}} \newcommand{\CJ}{\mathcal{J}} \newcommand{\RR}{\mathbb{R}} \newcommand{\NN}{\mathbb{N}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\ra}{\rightarrow} \newcommand{\la}{\leftarrow} \newcommand{\inv}{^{-1}} \newcommand{\maximize}{\mbox{maximize }} \newcommand{\minimize}{\mbox{minimize }} \newcommand{\subto}{\mbox{subject to }} \newcommand{\tr}{^{\intercal}} $
Introduction to Linear Optimization¶
In this first lecture, we shall review the basics of linear programming and talk about the difficulties associated with integer programming problems. We presume that you have a working knowledge of the simplex method and the notion of duality. The examples in these notes are taken mainly from two resources cited at the end of the lecture.
We can define a general optimization problem as follows:
$$ \begin{array}{lll} \minimize & f(x) & \\ \subto & g_i(x) \geq 0, & i=1, \dots, m, \end{array} $$where $f:\RR^n \ra \RR$ and $g_i:\RR^n \ra \RR$ for $i=1, \dots, m$. We call $f$ as the objective function and $g_i:\RR^n \ra \RR$ for $i=1, \dots, m$ as the constraint functions. Using these constraints, we have the feasible region given by
$$ \CF = \{x \in \RR^n : g_i(x) \geq 0, i=1, \dots, m\}. $$Thus, we can give an equivalent representation for our optimization problem as
$$ \begin{array}{rcll} v(\CF)& = & \minimize & f(x) \\ & & \subto & x \in \CF, & & \end{array} $$where $v(\CF)$ denotes the optimal objective function value attained over the feasible region $\CF$. Consider now two alternative feasible regions, $\CF^+$ and $\CF^-$, satisfying
$$ \CF^+ \subset \CF \subset \CF^-. $$Then, we obtain
$$ v(\CF^+) \geq v(\CF) \geq v(\CF^-). $$Typically, the feasible regions $\CF^+$ and $\CF^-$ are obtained by adding and removing constraints to the original feasible region $\CF$, respectively.
Linear Programming¶
When we talk about linear programming (LP), we mean that the objective function and the constraints of the above optimization problem are all linear functions. Therefore, we can compactly write a linear programming problem by using vectors and matrices
$$ \begin{array}{ll} \minimize & c\tr x \\ \subto & Ax = b, \\ & x \geq 0. \end{array} $$The mathematical model above is also known as a linear program in standard form. Note that in this form, we have only equalities and the nonnegativity constraints. This is not a restriction as it is fairly easy to convert any linear optimization problem into the standard form.
Here is a simple LP example:
$$ \begin{array}{ll} \maximize & 2x_1 - x_2 + x_3\\ \subto & 3x_1 + x_2 + x_3 + x_4 = 6, \\ & x_1 - x_2 + 2x_3 + x_5 = 1, \\ & x_1 + x_2 - x_3 + x_6 = 2, \\ & x_1, x_2, x_3, x_4, x_5, x_6 \geq 0. \end{array} $$We can solve the above example with GLPK in Octave. We first create the vectors and the matrices for our problem. Then, we just call the Octave linear programming solver glpk.
c = [2; -1; 1; 0; 0; 0]; % Objective function coefficients
Aeq = [3, 1, 1, 1, 0, 0; ...
1, -1, 2, 0, 1, 0; ...
1, 1, -1, 0, 0, 1]; % Coefficient matrix for equalities
beq = [6; 1; 2]; % RHS for equalities
lb = zeros(6, 1); ub = [];
ctype = repmat("S", 1, 3); vartype = repmat("C", 1, 6);
[x, fval, errnum] = glpk(c, Aeq, beq, lb, ub, ctype, vartype, -1);
fprintf('Solution Status = %d\n', errnum);
fprintf('Optimal Objective Function Value = %f\n', fval);
fprintf('Optimal Solution = '); disp(x')
Recall that we can obtain the optimal solution of an LP with the simplex method or the interior point method. In the coming lectures, we shall be using the fundamental ideas behind the simplex method. So, what is this simplex method?
Simplex Method¶
In a nutshell, the simplex method jumps from an extreme point to one of its neighbors that will improve the objective function. If there are no such neighbors, then the method terminates for the optimal solution is attained. An extreme point resides at the intersection of $n$ linearly independent constraint boundaries. From linear algebra point of view, the extreme points are associated with the bases.
To obtain a basis, we first select $m$ linearly independent columns from $A$ and form the matrix $B$. The remaining columns constitute the matrix $N$. The variables corresponding to $B$ and $N$ are denoted by $x_B$ and $x_N$ so that we can write
$$ Ax = Bx_B + Nx_N = b \\ z = c\tr x = c_B\tr x_B + c_N\tr x_N, $$where $z$ denotes the objective function value corresponding to solution $x$. Since $B$ is invertible, we can rewrite the above equalities as follows:
$$ \begin{array}{rcl} x_B & = & B\inv b - B\inv N x_N, \\ z & = & c_B\tr B\inv b + (c_N\tr - c_B\tr B\inv N)x_N. \end{array} $$This is known as a dictionary formed with $B$. The components of the vector $x_B$ are the basic variables and the components of the vector $x_N$ are nonbasic variables. In the simplex method, the nonbasic variables are all set to 0. Therefore, if we further have
$$ x_B = B\inv b \geq 0 $$then primal feasibility condition is satisfied, since
$$ x_B \geq 0 \mbox{ with } x_N = 0 \implies x \geq 0. $$At this point, we can jump to an adjacent extreme point by removing one column from $B$ and replacing it with a column in $N$. This is nothing but swapping the corresponding basic and nonbasic variables. In other words, the basic variable that corresponds to the leaving column becomes nonbasic and the nonbasic variable that corresponds to the entering column becomes basic. Notice that among the nonbasic variables, we would consider one of them only if it reduces the objective function value, $z$. Mathematically, the nonbasic variable $x_k$ can become basic, if
$$ (c_N\tr - c_B\tr B\inv N)_k < 0. $$The left-hand-side of the above inequality is known as the reduced cost of $x_k$. Clearly, the reduced costs of the basic variables are all zero:
$$ c_B\tr - c_B\tr B\inv B = 0. $$If there is no nonbasic variable with a negative reduced cost, then we cannot improve the objective function value any more. This is known as dual feasibility and its condition is given by
$$ c_N\tr - c_B\tr B\inv N \geq 0. $$For a given basis, if we both primal and dual feasibility conditions are satisfied, then we obtain the optimal solution.
Going back to our example, we can check primal and dual feasibility of the optimal solution.
% Basic variables: 1, 2, 4 & Nonbasic variables: 3, 5
bv = [1, 2, 4]; nbv = [3, 5];
B = Aeq(:, bv); N = Aeq(:, nbv);
cB = c(bv);
cN = c(nbv);
fprintf('Primal feasibility: '); disp((inv(B)*beq)');
fprintf('Dual feasibility: '); disp(cN' - cB'*inv(B)*N);
Duality¶
For each LP problem, there is a unique matching LP model known as the dual problem. A formal presentation of the duality theory is beyond the scope of this review. However, we can give a rough construction.
We can proceed with an example to illustrate our approach (Frenk, 2011). Consider the LP problem
$$ \begin{array}{lll} \minimize & 5x_1 + 11x_2 + 8x_3 & \\ \subto & 2x_1 + 3x_2 + 3x_3 \geq 7, \\ & 3x_1 + 7x_2 + 4x_3 \geq 11, \\ & x_1 + 2x_2 + 2x_3 \geq 5, \\ & x_1, x_2, x_3 \geq 0. \end{array} $$Suppose that instead of finding an optimal solution, we are interested in finding a good lower bound on the optimal objective function value of this LP problem. Here are a couple of observations:
If we multiply the first constraint by 2, then we obtain $$ 4x_1 + 6x_2 + 6x_3 \geq 14. $$ All variables are nonnegative and the coefficients of the variables in the objective function are all higher than the above inequality. Thus, $$ 14 \leq 4x_1 + 6x_2 + 6x_3 \leq 5x_1 + 11x_2 + 8x_3. $$ Then, 14 is our first lower bound.
Similarly, if we multiply the second constraint by 1, then we obtain $$ 11 \leq 3x_1 + 7x_2 + 4x_3 \leq 5x_1 + 11x_2 + 8x_3. $$ We now have our second lower bound as 11.
Using again the same idea, we multiply the third constraint by 4 and obtain $$ 20 \leq 4x_1 + 8x_2 + 8x_3 \leq 5x_1 + 11x_2 + 8x_3. $$ Our third lower bound is 20.
Clearly, among these three lower bounds, the tightest one is the third one as it gives the maximum lower bound. However, these bounds are obtained by using multipliers 2, 1 and 4 for the three constraints, respectively. Where do these multipliers come from? Are there alternate multipliers, which would produce better lower bounds? Let's call these multipliers as $y_1$, $y_2$ and $y_3$. Then, we have
$$ (2x_1 + 3x_2 + 3x_3)y_1 \geq 7y_1, \\ (3x_1 + 7x_2 + 4x_3)y_2 \geq 11y_2, \\ (x_1 + 2x_2 + 2x_3)y_3 \geq 5y_3, $$This leads to
$$ (2x_1 + 3x_2 + 3x_3)y_1 + (3x_1 + 7x_2 + 4x_3)y_2 + (x_1 + 2x_2 + 2x_3)y_3 \geq 7y_1 + 11y_2 + 5y_3, $$which we can rewrite as
$$ (2y_1 + 3y_2 + 2y_3)x_1 + (3y_1 + 7y_2 + 2y_3)x_2 + (3y_1 + 4y_2 + 2y_3)x_3 \geq 7y_1 + 11y_2 + 5y_3. $$Recall that the objective function was $5x_1 + 11x_2 + 8x_3$. Thus, we want
$$ \underset{\leq 5}{\underbrace{(2y_1 + 3y_2 + 2y_3)}}x_1 + \underset{\leq 11}{\underbrace{(3y_1 + 7y_2 + 2y_3)}}x_2 + \underset{\leq 8}{\underbrace{(3y_1 + 4y_2 + 2y_3)}}x_3 \geq \underset{\mbox{as large as possible}}{\underbrace{7y_1 + 11y_2 + 5y_3}}. $$After the discussion above, it seems that we can write an LP to obtain the best lower bound. Here it is:
$$ \begin{array}{lll} \maximize & 7y_1 + 11y_2 + 5y_3 & \\ \subto & 2y_1 + 3y_2 + y_3 \leq 5, \\ & 3y_1 + 7y_2 + 2y_3 \leq 11, \\ & 3y_1 + 4y_2 + 2y_3 \leq 8, \\ & y_1, y_2, y_3 \geq 0. \end{array} $$Of course, the optimal solution to this LP problem also gives a lower bound for the original LP problem. In LP, one of these two models is called the primal problem and then, the other one is called the dual problem.
Let's solve both problems with GLPK.
% First the "primal" problem.
c = [5; 11; 8];
Aineq = [2, 3, 3; ...
3, 7, 4; ...
1, 2, 2];
bineq = [7; 11; 5];
lb = zeros(3, 1); ub = [];
ctype = repmat("L", 1, 3); vartype = repmat("C", 1, 3);
[x, fval] = glpk(c, Aineq, bineq, lb, ub, ctype, vartype, 1);
fprintf('Optimal Objective Function Value of the Primal Problem= %f\n', fval);
fprintf('Optimal Solution of the Primal Problem= '); disp(x')
% Next the "dual" problem.
ctype = repmat("U", 1, 3);
[y, fval] = glpk(bineq, Aineq', c, lb, ub, ctype, vartype, -1);
fprintf('Optimal Objective Function Value of the Dual Problem= %f\n', fval);
fprintf('Optimal Solution of the Dual Problem= '); disp(y')
Note that both problems give the same optimal objective function value. To formalize this observation, let us first write both models in matrix notation:
$$ \begin{array}{rllcrll} z_P = & \minimize & c\tr x & & z_D = & \maximize & y\tr b & \\ & \subto & Ax \geq b, & & & \subto & A\tr y \leq c,\\ & & x \geq 0. & & & & y \geq 0. \end{array} $$Here the primal problem has $n$ variables and $m$ constraints, whereas the dual problem has $m$ variables and $n$ constraints.
Our discussion about bounding hints that $z_P \geq z_D$. This is indeed true when both problems have nonempty feasible regions, and the result is known as the weak duality. In fact, if both problems have nonempty feasible regions, then after a little bit of work we can also show the strong duality result:
$$ z_P = z_D. $$Homework 1: Show the relationship between the reduced cost of a variable in the primal problem and the feasibility of the corresponding dual constraint.
Mixed Integer Programming¶
Given an LP problem, if some of all of the variables are restricted to be integer values, then we are in the domain of mixed integer programming (MIP). Although the difference between an LP problem and a MIP problem is so little, it turns out that plenty of MIP problems are notoriously difficult to solve.
Consider, for instance, the following pure integer programming (IP) problem (Hillier and Lieberman, 2005):
$$ \begin{array}{lll} \maximize & x_2 & \\ \subto & -2x_1 + 2x_2 \leq 1, \\ & 2x_1 + 2x_2 \leq 7, \\ & x_1, x_2 \geq 0, \\ & x_1, x_2 \mbox{ integers}. \end{array} $$We shall call the last restriction as the integrality constraint. Of course, this is a tiny problem that we can solve with CPLEX in no time. But suppose for the sake of our discussion that we were unable to solve this problem, instead we ignore the integrality constraint and solve the resulting LP problem. This is called LP relaxation. Since, we are removing a constraint, the optimal objective function of the LP relaxation constitutes an upper bound on the optimal objective function value of the IP problem. This holds as we have a maximization problem. If we were instead solving a minimization problem, then the optimal objective function value of the LP relaxation would give a lower bound.
c = [0; 1];
Aineq = [-2, 2; ...
2, 2];
bineq = [1; 7];
lb = zeros(2, 1); ub = [];
ctype = repmat("U", 1, 2); vartype = repmat("C", 1, 2);
% First LP solution
[x, fval_lp] = glpk(c, Aineq, bineq, lb, ub, ctype, vartype, -1);
fprintf('Optimal Objective Function Value of LP = %f\n', fval_lp);
fprintf('Optimal Solution of LP = '); disp(x')
vartype = repmat("I", 1, 2); % Both variables are required to be integer
[x, fval_ip] = glpk (c, Aineq, bineq, lb, ub, ctype, vartype, -1);
fprintf('Optimal Objective Function Value of IP = %f\n', fval_ip);
fprintf('Optimal Solution of IP = '); disp(x')
fprintf('Relative gap = %.0f%%', 100*(fval_lp/fval_ip));
Suppose that we also have a feasible solution for the IP problem, then the objective function value of this feasible solution clearly gives a lower bound. If the upper and the lower bounds are close to each other, then we can infer that the current feasible solution is close to the actual optimum. Otherwise, it is not possible to make a conclusive statement. For instance, in the above example, if we use the LP relaxation for upper bounding, then even with the actual optimal solution of IP, we can not state that it is an optimal solution because there is a huge relative gap between the optimal objective function values of LP and IP.
Then, the next question is how to find a feasible IP solution? One simple approach is called rounding. If the decision variables, which are restricted to be integers, attain fractional values after solving the LP relaxation, they are rounded up or down to make them integral. There are two major caveats to this approach: (i) The rounded solution may not be feasible. (ii) The objective function value of the rounded solution may yield a poor lower bound. The figure below illustrates the first case.
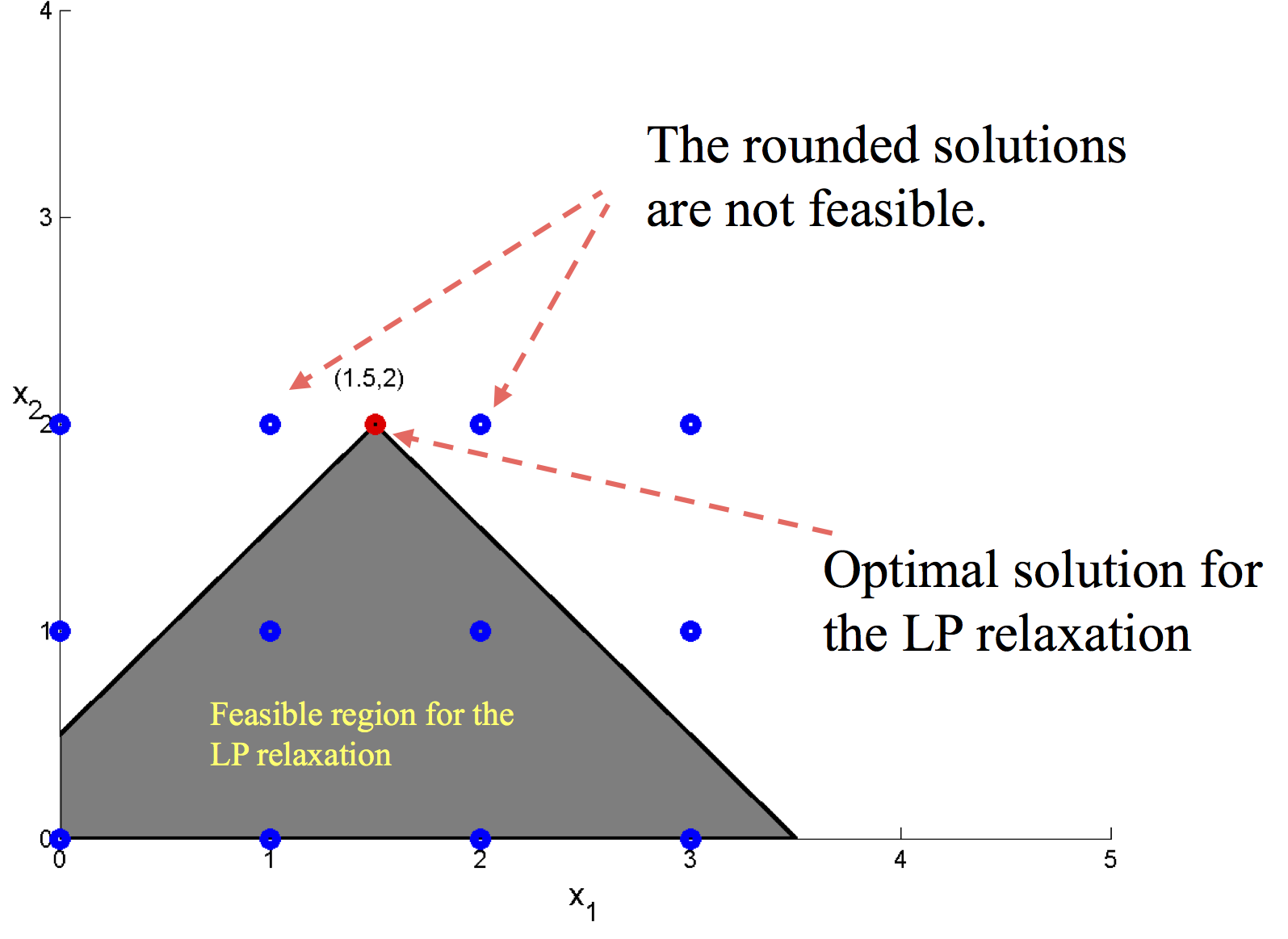
There are several different methods to solve MIP problems. If such a method claims to find the exact optimal solution for any MIP problem, then with our current technology, you can be sure that the algorithm may take a very very long time to find the optimal solution. In fact most of those algorithms do -one way or another- an exhaustive enumeration. A simple but a very well-known enumeration algorithm is explained next.
Branch and Bound (B&B) Algorithm¶
The main idea of B&B algorithm is to divide the original problem into smaller subproblems by splitting the set of feasible solutions. The splitting continues until the subproblem is eliminated by bounding. The splitting is called as branching whereas the elimination of subproblems is known as fathoming. During the iterations of B&B algorithm, some subproblems attain solutions that are feasible for the original MIP problem, then among those solutions the best one is kept as the incumbent solution. In short, there are three main steps in B&B algorithm: branching, bounding and fathoming. In this section, we assume that the bounding is carried out by solving the LP relaxations of the subproblems.
Here is an outline of the B&B algorithm for solving a MIP problem with maximization objective:
- Initialization: Set $Z^* = -\infty$.
- Iterations:
- Branching: Among the unfathomed subproblems, pick one and branch into two new subproblems by introducing two new constraints.
- Bounding: Solve LP relaxation for each subproblem.
- Fathoming: Apply the following three fathoming steps to each sbproblem and eliminate the fathomed subproblems.
- (F1) Obtained bound by the subproblem is less than or equal to $Z^*$.
- (F2) LP relaxation of the subproblem is infeasible.
- (F3) The optimal solution of the subproblem gives a feasible solution for the original MIP problem. If this solution becomes the new incumbent, update $Z^*$ and apply (F1) to all unfathomed subproblems.
- Optimality: If there are no unfathomed problems, then the incumbent solution is the optimal one. Otherwise, do one more iteration.
Notice that in the bounding step (2.A) above, we are reoptimizing a subproblem after adding only one constraint. This step can be quite efficiently handled by using the dual simplex method as we are only adding one column to the dual of the subproblem.
Let us apply the B&B algorithm to the following problem $$ \begin{array}{ll} \maximize & 4x_1 - 2x_2 + 7x_3 - x_4\\ \subto & x_1 + 5x_3 \leq 10, \\ & x_1 + x_2 - x_3 \leq 1, \\ & 6x_1 - 5x_2 \leq 0, \\ & -x_1 + 2x_3 - 2x_4 \leq 3, \\ & x_1, x_2, x_3, x_4 \geq 0, \\ & x_1, x_2, x_3 \mbox{ integers}. \\ \end{array} $$
The root problem is simply LP relaxation of the above problem.
% Root problem
c = [4; -2; 7; -1];
Aineq = [ 1, 0, 5, 0; ...
1, 1, -1, 0; ...
6, -5, 0, 0; ...
-1, 0, 2, -2];
bineq = [10; 1; 0; 3];
lb = zeros(4, 1); ub = [];
ctype = repmat("U", 1, 4); vartype = repmat("C", 1, 4);
[x, fval, errnum] = glpk(c, Aineq, bineq, lb, ub, ctype, vartype, -1);
fprintf('Solution Status = %d\n', errnum);
fprintf('Optimal Objective Function Value of the Root Problem = %f\n', fval);
fprintf('Optimal Solution of the Root Problem = '); disp(x')
None of the first three variables is integer. We branch from $x_1$ and obtain the following two subproblems:
$$ \begin{array}{llcll} \maximize & 4x_1 - 2x_2 + 7x_3 - x_4 & \hspace{5mm}& \maximize & 4x_1 - 2x_2 + 7x_3 - x_4\\ \subto & x_1 + 5x_3 \leq 10, & & \subto & x_1 + 5x_3 \leq 10, \\ & x_1 + x_2 - x_3 \leq 1, & & & x_1 + x_2 - x_3 \leq 1,\\ & 6x_1 - 5x_2 \leq 0, & & & 6x_1 - 5x_2 \leq 0,\\ & -x_1 + 2x_3 - 2x_4 \leq 3, & & & -x_1 + 2x_3 - 2x_4 \leq 3,\\ & x_1, x_2, x_3, x_4 \geq 0, & & & x_1, x_2, x_3, x_4 \geq 0,\\ & \mathbf{x_1 \leq 1}, & & & \mathbf{x_1 \geq 2},\\ & x_1, x_2, x_3 \mbox{ integers}. & & & x_1, x_2, x_3 \mbox{ integers}.\\ \end{array} $$In other words, we have
- Subproblem 1: Original problem plus additional constraint $x_1 \leq 1$,
- Subproblem 2: Original problem plus additional constraint $x_1 \geq 2$.
Let's solve them quickly.
c = [4; -2; 7; -1];
% Subproblem 1
Aineq = [ 1, 0, 5, 0; ...
1, 1, -1, 0; ...
6, -5, 0, 0; ...
-1, 0, 2, -2; ...
1, 0, 0, 0];
bineq = [10; 1; 0; 3; 1];
lb = zeros(4, 1); ub = [];
ctype = repmat("U", 1, 5); vartype = repmat("C", 1, 4);
[x, fval, errnum] = glpk(c, Aineq, bineq, lb, ub, ctype, vartype, -1);
fprintf('Solution Status = %d\n', errnum);
fprintf('Optimal Objective Function Value of Subproblem 1 = %f\n', fval);
fprintf('Optimal Solution of Subproblem 1 = '); disp(x')
% Subproblem 2
Aineq = [ 1, 0, 5, 0; ...
1, 1, -1, 0; ...
6, -5, 0, 0; ...
-1, 0, 2, -2; ...
-1, 0, 0, 0];
bineq = [10; 1; 0; 3; -2];
[x, fval, errnum] = glpk(c, Aineq, bineq, lb, ub, ctype, vartype, -1);
fprintf('Solution Status = %d\n', errnum);
fprintf('Optimal Objective Function Value of Subproblem 2 = %f\n', fval);
fprintf('Optimal Solution of Subproblem 2 = '); disp(x')
So subproblem 2 is infeasible (solution status 10), and hence it is fathomed (F2). After solving subproblem 1, $x_1$ is integer but $x_2$ and $x_2$ ara still fractional. We next branch by using $x_2$ and obtain two new subproblems from subproblem 1:
- Subproblem 3: Original problem plus additional constraints $x_1 \leq 1$ and $x_2 \leq 1$,
- Subproblem 4: Original problem plus additional constraints $x_1 \leq 1$ and $x_2 \geq 2$.
c = [4; -2; 7; -1];
% Subproblem 3
Aineq = [ 1, 0, 5, 0; ...
1, 1, -1, 0; ...
6, -5, 0, 0; ...
-1, 0, 2, -2; ...
1, 0, 0, 0; ...
0, 1, 0, 0];
bineq = [10; 1; 0; 3; 1; 1];
lb = zeros(4, 1); ub = [];
ctype = repmat("U", 1, 6); vartype = repmat("C", 1, 4);
[x, fval, errnum] = glpk(c, Aineq, bineq, lb, ub, ctype, vartype, -1);
fprintf('Solution Status = %d\n', errnum);
fprintf('Optimal Objective Function Value of Subproblem 3 = %f\n', fval);
fprintf('Optimal Solution of Subproblem 3 = '); disp(x')
% Subproblem 4
Aineq = [ 1, 0, 5, 0; ...
1, 1, -1, 0; ...
6, -5, 0, 0; ...
-1, 0, 2, -2; ...
1, 0, 0, 0; ...
0, -1, 0, 0];
bineq = [10; 1; 0; 3; 1; -2];
[x, fval, errnum] = glpk(c, Aineq, bineq, lb, ub, ctype, vartype, -1);
fprintf('Solution Status = %d\n', errnum);
fprintf('Optimal Objective Function Value of Subproblem 4 = %f\n', fval);
fprintf('Optimal Solution of Subproblem 4 = '); disp(x')
After solving subproblems 3 and 4, $x_1$ and $x_3$ remain fractional. We pick $x_1$ and branch from subproblem 3:
- Subproblem 5: Original problem plus additional constraints $x_1 \leq 1$, $x_2 \leq 1$ and $x_1 \leq 0$ ($x_1=0$),
- Subproblem 6: Original problem plus additional constraints $x_1 \leq 1$, $x_2 \leq 1$ and $x_1 \geq 1$ ($x_1=1$).
c = [4; -2; 7; -1];
% Subproblem 5
Aineq = [ 1, 0, 5, 0; ...
1, 1, -1, 0; ...
6, -5, 0, 0; ...
-1, 0, 2, -2; ...
1, 0, 0, 0; ...
0, 1, 0, 0; ...
1, 0, 0, 0];
bineq = [10; 1; 0; 3; 1; 1; 0];
lb = zeros(4, 1); ub = [];
ctype = repmat("U", 1, 7); vartype = repmat("C", 1, 4);
[x, fval, errnum] = glpk(c, Aineq, bineq, lb, ub, ctype, vartype, -1);
fprintf('Solution Status = %d\n', errnum);
fprintf('Optimal Objective Function Value of Subproblem 5 = %f\n', fval);
fprintf('Optimal Solution of Subproblem 5 = '); disp(x')
% Subproblem 6
Aineq = [ 1, 0, 5, 0; ...
1, 1, -1, 0; ...
6, -5, 0, 0; ...
-1, 0, 2, -2; ...
1, 0, 0, 0; ...
0, 1, 0, 0; ...
-1, 0, 0, 0];
bineq = [10; 1; 0; 3; 1; 1; -1];
[x, fval, errnum] = glpk(c, Aineq, bineq, lb, ub, ctype, vartype, -1);
fprintf('Solution Status = %s\n', errnum);
fprintf('Optimal Objective Function Value of Subproblem 6 = %f\n', fval);
fprintf('Optimal Solution of Subproblem 6 = '); disp(x')
Subproblem 5 returns our first incumbent solution and hence it is fathomed. Moreover, the objective function value of this incumbent is higher than the bound obtained in subproblem 4. Therefore, we can also fathom subproblem 4 (F1). Since subproblem 6 is infeasible, all problems are fathomed and we have the optimal solution. The following figure shows iterations on a tree plot.
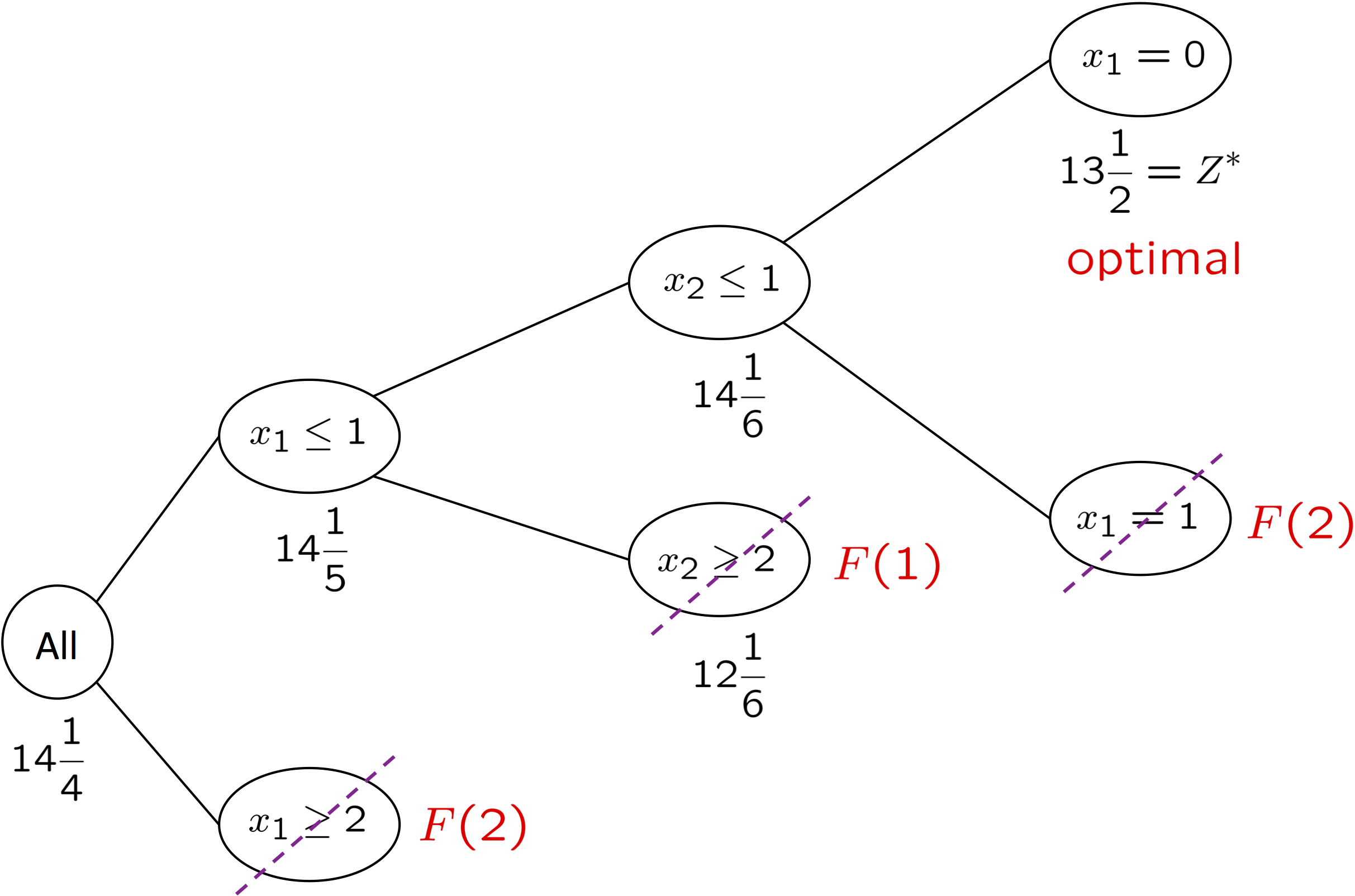
Let's double-check our result and conclude this lecture.
% Root problem
c = [4; -2; 7; -1];
Aineq = [ 1, 0, 5, 0; ...
1, 1, -1, 0; ...
6, -5, 0, 0; ...
-1, 0, 2, -2];
bineq = [10; 1; 0; 3];
lb = zeros(4, 1); ub = [];
ctype = repmat("U", 1, 4); vartype = "IIIC";
[x, fval_ip, errnum] = glpk(c, Aineq, bineq, lb, ub, ctype, vartype, -1);
fprintf('Optimal Objective Function Value of IP = %f\n', fval_ip);
fprintf('Optimal Solution of IP = '); disp(x')
References¶
- Hillier, F. S. and G. J. Lieberman (2005). Introduction to Operations Research, 8th Edition, NY: McGraw-Hill.
- Frenk, J. B. G. (2011). IE 301 Class Notes, Sabancı University.